Learning the Intensity of Time Events with Change-Points

M. Z. Alaya, S. Gaïffas, A. Guilloux

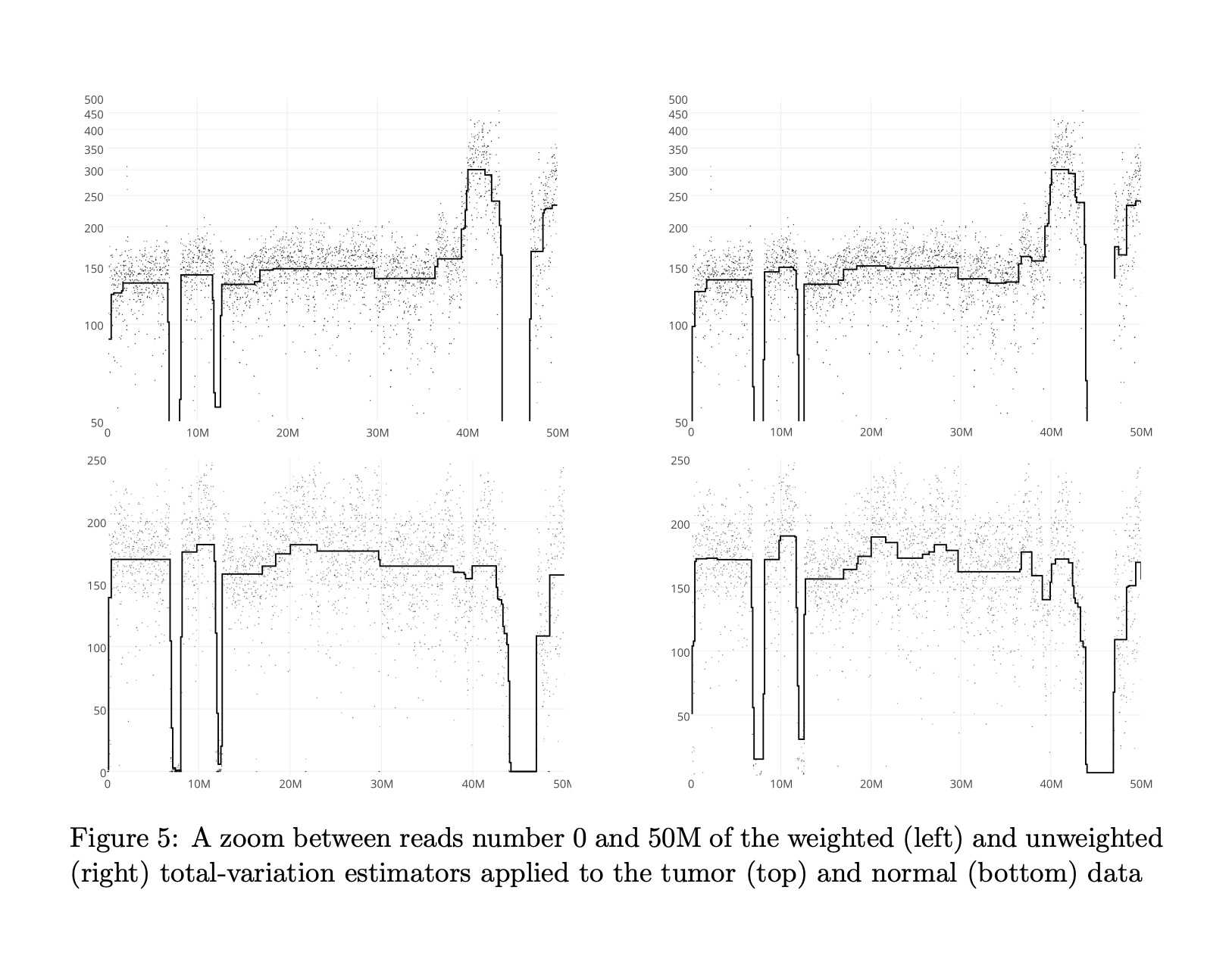
We consider the problem of learning the inhomogeneous intensity of a counting process, under a sparse segmentation assumption. We introduce a weighted total-variation penalization, using data-driven weights that correctly scale the penalization along the observation interval. We prove that this leads to a sharp tuning of the convex relaxation of the segmentation prior, by stating oracle inequalities with fast rates of convergence, and consistency for change-points detection. This provides first theoretical guarantees for segmentation with a convex proxy beyond the standard i.i.d signal + white noise setting. We introduce a fast algorithm to solve this convex problem. Numerical experiments illustrate our approach on simulated and on a high-frequency genomics dataset.

Download paper here