Theoretical Guarantees for Bridging Metric Measure Embedding and Optimal Transport

M. Z. Alaya, M. Bérar, G. Gasso, A. Rakotomamonjy

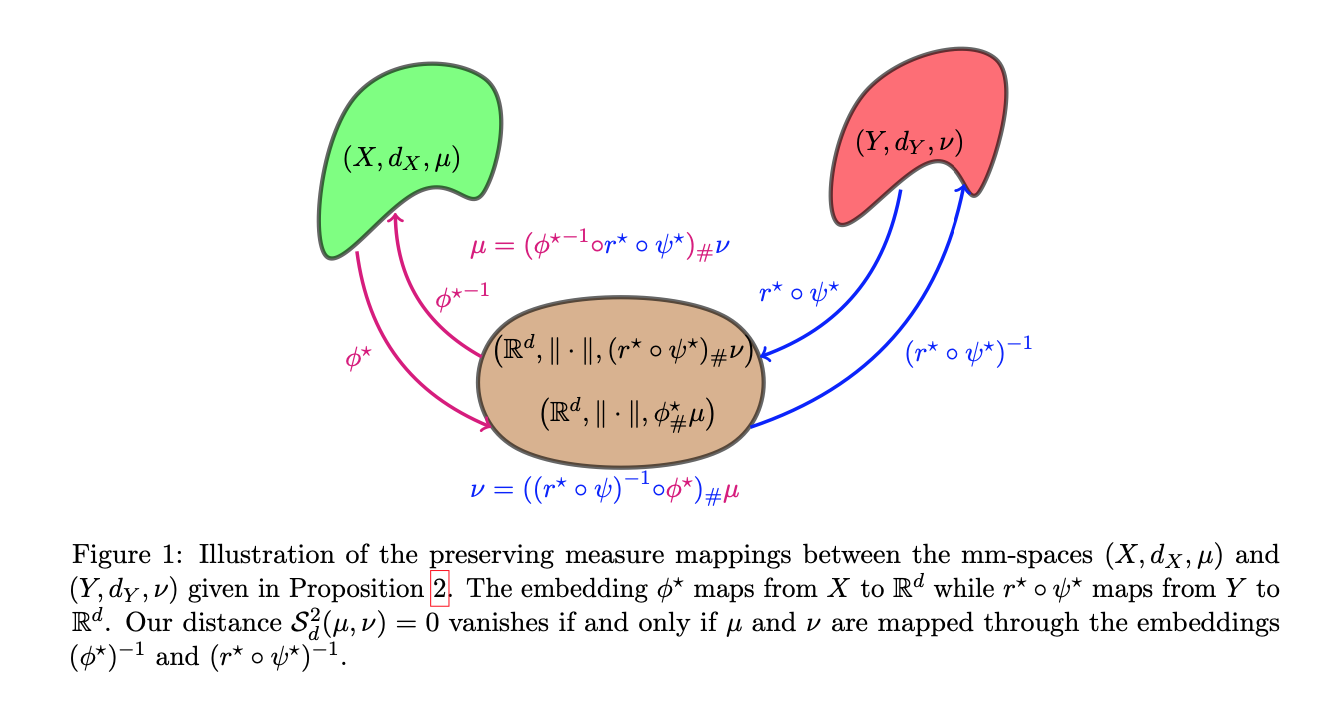
We propose a novel approach for comparing distributions whose supports do not necessarily lie on the same metric space. Unlike Gromov-Wasserstein (GW) distance which compares pairwise distances of elements from each distribution, we consider a method allowing to embed the metric measure spaces in a common Euclidean space and compute an optimal transport (OT) on the embedded distributions. This leads to what we call a sub-embedding robust Wasserstein (SERW) distance. Under some conditions, SERW is a distance that considers an OT distance of the (low- distorted) embedded distributions using a common metric. In addition to this novel proposal that generalizes several recent OT works, our contributions stands on several theoretical analyses: (i) we characterize the embedding spaces to define SERW distance for distribution alignment; (ii) we prove that SERW mimics almost the same properties of GW distance, and we give a cost relation between GW and SERW. The paper also provides some numerical illustrations of how SERW behaves on matching problems.

Download paper here