Bio
Welcome to my homepage! Since September 2020, I am Maître de Conférences (≈ Assistant Professor) of Statistics and Machine Learning at Université de Technologie de Compiègne (UTC). I teach in Computer Science Department and I do my research in laboratory of Applied Mathematics (LMAC) .
From Jan. 2019 to Aug. 2020, I was a postdoctoral researcher in LITIS Laboratory at Université de Rouen, working with Professors Maxime Bérar, Gilles Gasso, and Alain Rakotomamonjy. I was involved in OATMIL Project, which aims at bridging optimal transport and machine learning.
In 2017-2018, I was a laureate of Postdoctoral Fellowship Program DIM Math Innov Région Ile-de-France. I was hosted in Modal'X laboratory at Université Paris Nanterre working with Professor Olga Klopp on collective matrix completion project.
I received my PhD in Statistical Machine Learning from University Pierre and Marie Curie on June 27th, 2016 under the supervision of Professors Stéphane Gaïffas and Agathe Guilloux. My doctoral thesis is centered around studying supervised learning in high-dimensional settings using weighted total-variation penalization.
News
- Jan. 2026. Paper A Unified Kantorovich Duality for Multimarginal Optimal Transport. Submitted.
- Jan. 2026.Paper Optimal Transport Guarantees to Nonparametric Regression for Locally Stationary Time Series. Artificial Intelligence and Statistics Conference, AISTATS 2026.
- Jan. 2026.Paper Unmixing Mean Embeddings for Domain Adaptation with Target Label Proportion. Artificial Intelligence and Statistics Conference, AISTATS 2026.
- Nov. 2025. Paper Application of Convolution Neural Network for Unfolding Simulated Neutron Spectra of an Activation Spectrometer. IEEE Transactions on Nuclear Science.
- Sep. 2025. Paper PatchTrAD: A Patch-Based Transformer focusing on Patch-Wise Reconstruction Error for Time Series Anomaly Detection. European Signal Processing Conference, EUSIPCO 2025. .
Academic Positions
-
2020 Present
Maître de Conférences
Laboratory LMAC
Department Computer Science
Univeristy of Technology of Compiègne
-
2018 2020
Postdoctoral Researcher
LITIS Laboratory
University Rouen Normandy
-
2017 2018
Postdoctoral Researcher
Modal'X Laboratory
University Paris Nanterre
-
2017 2016
Temporary Teaching Researcher Assistant
Modal'X Laboratory
University Paris Nanterre
Education
-
Ph.D. 2016
Ph.D. in Statistics Machine Learning
Departement of Statistics LSTA
University Pierre and Marie Curie
-
Master2012
Master of Sciences in Statistics
University Pierre and Marie Curie
-
Master2011
Master of Sciences in Probabilities and Random Modelling
University Pierre and Marie Curie
-
Magisterium2010
Magisterium of Mathematics
University Gabes Tunisia
Mokhtar Z. Alaya
PhD in Statistics Machine Learning (2012-2016)
- University Pierre and Marie Curie
- title: Segmentation of Counting Processes and Dynamical Models
- Thesis defended on June 27th 2016 before a jury composed of: Pierre Alquier (ENSAE), Examiner; Sylvain Arlot (Univ. Paris-Sud), Examiner; Gérard Biau (UPMC), Examiner; Stéphane Gaïffas (Univ. Paris Diderot), Advisor; Agathe Guilloux (Univ. Evry), Advisor; Erwan Le Pennec (École Polytechnique), Reviewer
-
 Manuscript,
Manuscript,
 Slides
Slides
MSc in Applied Mathematics, speciality Statistics (2011-2012)
- University Pierre and Marie Curie
- Master thesis: Change-Points Detection with Total-Variation Penalization
- Under the supervision of Stéphane Gaïffas (Univ. Paris Diderot) and Agathe Guilloux (Univ. Evry)
-
 Manuscript
Manuscript
MSc in Applied Mathematics, speciality Probabilities and Random Models (2010-2011)
- University Pierre and Marie Curie
- Master thesis: Poisson Access Networks with Shadowing: Modeling and Statistical Inference
- Under the supervision of Bartlomiej Blaszczyszyn (INRIA) and Mohamed Karray (Orange Labs)
-
 Manuscript,
Manuscript,
 Slides
Slides
Magisterium of Mathematics (2008-2010)
- University of Gabes, Tunisia
- Magisterium thesis: Backward Stochastic Differential Equations and Financial Mathematics
- Under the supervision of Said Hamadène (Univ. Le Mans) and Ibtissem Hdhiri (Univ. Gabes)
-
 Manuscript,
Manuscript,
 Slides
Slides
BSc in Mathematics (2005-2007)
- University of Gabes, Tunisia
Undergraduate in Mathematics and Computer Science (2003-2005)
- University of Gabes, Tunisia
Teaching
Interacting with students is one of the most important components of any academic career. During my teaching experience in diverse universities, I have taught mathematics, statistics and machine learning at all levels, both to students within the field and to students from other disciplines.
University of Technology of Compiègne
-
2021-2025AI28 - Machine LearningMachine learning (apprentissage automatique ou apprentissage machine) est une branche de l’intelligence artificielle (IA), qui est elle même une branche de la science de données. Ce cours est conçu pour faire une présentation des méthodologies et algorithmes de machine learning, dans leurs concepts comme dans leurs cas typiques d’applications. La mise en ouvre de ces concepts se fait en langage de programmation Python.
Partie 1: Introduction générale au machine learrning et prise en main de Python
Partie 2 : Formalisme mathématique d’un problème de machine learning
Partie 3 : Apprentissage supervisé
Partie 4 : Apprentissage non-supervisé
-
2025Applied Machine Learning for Process EngineeringMachine learning appliqué pour le génies des procédés.
1. Introduction générale au machine learning
2. Librairie Python : Pandas, Scipy, Matplotlib, Pyplot, Seaborn
3. Régression linéaire multiple, Régression pénalisée, SVM, Arbres de décision, Forêts aléatoires
4. Réduction de la dimension, Analyse en composantes principales (ACP), Clustering
5. Applications sur des données chimiques réelles
-
2020-2022MT23 - Linear Algebra and ApplicationsBases d’algèbre linéaire; diagonalisation, trigonalisaiton et applications pour des systèmes d’équations différentielles.
-
2022-2025MT02 - Real AnalysisPremier volet du module initial de mathématiques de Tronc Commun. Il permet d'acquérir les bases indispensables à l'étude des fonctions d'une variable.
-
2022-2023MT11 - Real Analysis and AlgebraSynthèse des mathématiques du premier cycle: fonctions d’une ou plusieurs variables, courbes et surfaces, intégrales simples et multiples, équations différentielles, bases de l’algèbre linéaire. L’enseignement se présente sous forme d’un cours-TD fondé sur un document intégrant cours et exercices.
-
2022-2023MT22 - Multivariate CalculusContinuité, différentiabilité des fonctions de plusieurs variables réelles. Analyse vectorielle. Courbes et surfaces de \(\mathbb{R}^3\). Intégrales multiples ; curvilignes, surfaciques. Théorèmes intégraux.
-
2021-2022SY01 - ProbabilityNotion d’aléatoire et introduction au calcul des probabilités.
University of Paris Nanterre
-
2016-2017StatisticsReal Analysis and C2I Certificate
University of Pierre Marie Curie
-
2015-2016Mathematical StatisticsTimes Series
-
2012-2014Linear Models IIProbability and StatisticsAlgebra and Geometry
Research Summary
My research topics are statistical machine learning, with a particular interest in sparse inference, matrix completion and survival analysis. Currently, I am interested in optimal transport techniques for machine learning applications.
Research Interests
- Statistical Machine Learning Theory & Applications
- Machine Learning (ML) and Deep Learning (DL)
- Optimal Transport for ML/DL
- High-dimensional Statistics
- Matrix Completion
- Data Science
Research Projects
-
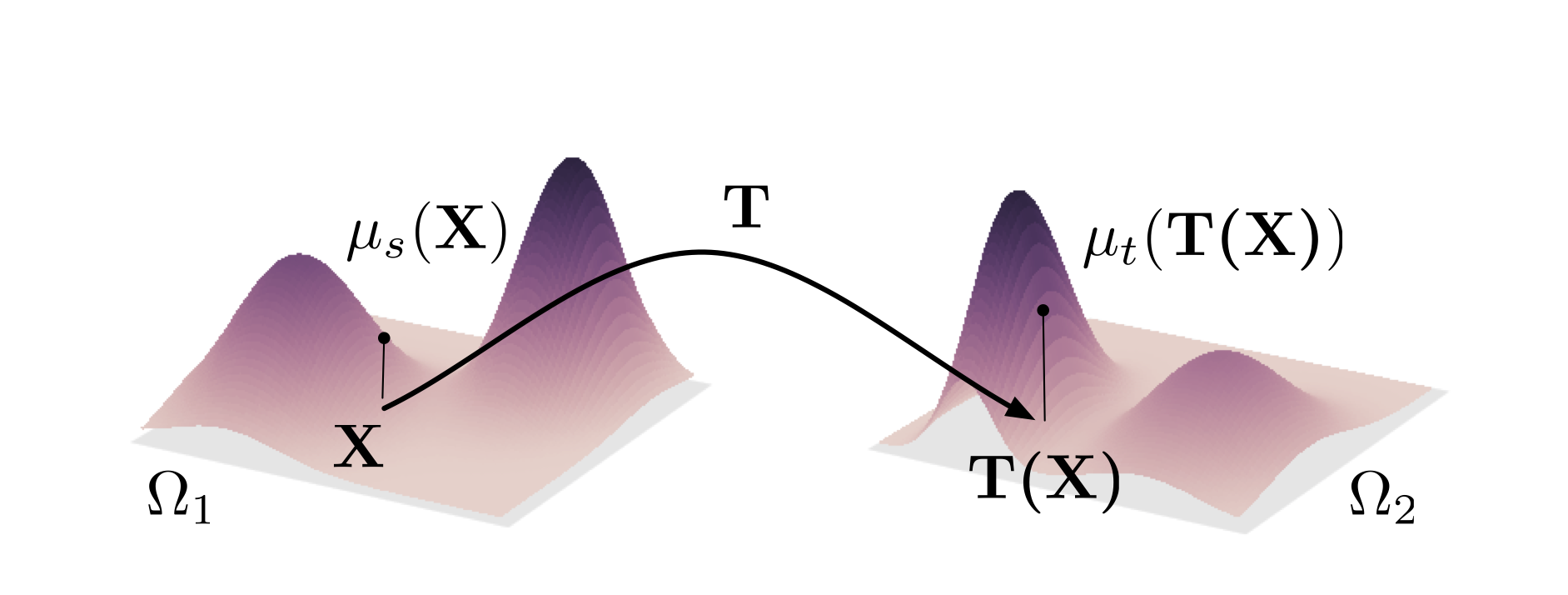
Bridging Machine Learning and Optimal Transport
Optimal transport (OT) based data analysis has proven a significant usefulness to achieve many central tasks in machine learning, statistics, computer vision, among many others. This success is due to the natural geometric comparison framework offered by OT toolboxes. In a nutshell, OT is mathematical tool to compare distributions by computing a transportation mass plan from a source to a target distribution. Distances based on OT are referred to as the Wasserstein distance and have been successfully employed in a wide variety of machine learning.
-
High-dimensional Statistical Learning
Availability of massive data in high-dimension, namely when the number of features (covariates) is much larger than the number of observations, arises in diverse fields of sciences, ranging from computational biology and health studies to financial engineering and risk management, to name a few. These data have presented serious challenges to existing learning methods and reshaped statistical thinking and data analysis. To address the curse of dimensionality problem, sparse inference is now an ubiquitous technique for dimension reduction} and variable selection. Sparse solution generally helps in better interpretation of the model and more importantly leads to better generalization on unseen data. A fundamental step in sparsity is to do careful variable selection based on the idea of adding apenalty term on the model complexity to some goodness-of-fit.
Interdisciplinary Project: Artificial Intelligence for Mecanic (AI4Meca)
-
2024-2025Unsupervised Deep Clustering of combined data from multi-Structural Health Monitoring Techniques obtained on Smart Polymer-Matrix Composites embedded with Piezoelectric Transducers
 This project is a first collaboration with Matériaux et Surfaces team of Roberval Laboratory in UTC. It concerns data fusion and clustering methods utilizing deep neural networks (DNN) to classify heterogeneous data from different acquisition methods. A machine learning algorithm, specifically a convolutional autoencoder, was evaluated by clustering datasets obtained from load-unload tensile tests of smart specimens embedding PZTs and PVDF transducers. These piezoelectric transducers were employed to collect multi-source data for SHM purposes. Additionally, external equipment such as DIC and AE were used for both validation and the initial testing of the DNN configuration. The project highlights the feasibility of using DNN architecture to classify multi-acquired and merged data for SHM.
This project is a first collaboration with Matériaux et Surfaces team of Roberval Laboratory in UTC. It concerns data fusion and clustering methods utilizing deep neural networks (DNN) to classify heterogeneous data from different acquisition methods. A machine learning algorithm, specifically a convolutional autoencoder, was evaluated by clustering datasets obtained from load-unload tensile tests of smart specimens embedding PZTs and PVDF transducers. These piezoelectric transducers were employed to collect multi-source data for SHM purposes. Additionally, external equipment such as DIC and AE were used for both validation and the initial testing of the DNN configuration. The project highlights the feasibility of using DNN architecture to classify multi-acquired and merged data for SHM. -
2025-2028Generative Deep Learning for Atomistically Engineered Materials: Synergistic Integration of Molecular Dynamics Simulations, Experiments and Data Augmentation
 This project is a second collaboration with Matériaux et Surfaces team of Roberval Laboratory in UTC. The primary objective of the project is to advance the development of nanostructured materials with tailored properties through novel approaches. It proposes an integrated, data-driven approach to expedite the development of advanced nanostructured materials. Using machine learning-driven data augmentation—specifically GANs, VAEs, and hybrid architectures—we address the constraints of limited datasets in materials science. This strategy complements existing experimental and atomistic modeling efforts, allowing robust predictions of material behavior across scales. It reduces time and cost associated with iterative experimentation and simulation. Moving forward, deeper validation of the synthetic data’s physical relevance—via experiments and atomistic simulations—will be crucial.
This project is a second collaboration with Matériaux et Surfaces team of Roberval Laboratory in UTC. The primary objective of the project is to advance the development of nanostructured materials with tailored properties through novel approaches. It proposes an integrated, data-driven approach to expedite the development of advanced nanostructured materials. Using machine learning-driven data augmentation—specifically GANs, VAEs, and hybrid architectures—we address the constraints of limited datasets in materials science. This strategy complements existing experimental and atomistic modeling efforts, allowing robust predictions of material behavior across scales. It reduces time and cost associated with iterative experimentation and simulation. Moving forward, deeper validation of the synthetic data’s physical relevance—via experiments and atomistic simulations—will be crucial.
Interdisciplinary Project: Artificial Intelligence for Chemical (AI4Chem)
-
2025-2026Machine Learning Prediction Modelling for Chemistry with emphasis on High-Through Experiment
 This project is a collaboration with the team Activités Microbiennes et Bioprocédés (MAB) of TIMR Laboratory U High-throughput experimentation in chemistry enables rapid and automated exploration of chem- ical space, facilitating the discovery of new drugs. Integrating machine learning techniques with these high-throughput methods can further accelerate and enhance the exploration and optimization of chemical space.
This project is a collaboration with the team Activités Microbiennes et Bioprocédés (MAB) of TIMR Laboratory U High-throughput experimentation in chemistry enables rapid and automated exploration of chem- ical space, facilitating the discovery of new drugs. Integrating machine learning techniques with these high-throughput methods can further accelerate and enhance the exploration and optimization of chemical space.
Papers
Publishing high-quality papers has always been my constant goal.
Filter by type:
Sort by year:
A Unified Kantorovich Duality for Multimarginal Optimal Transport.
Yehya Charyala, Mokhtar Z. Alaya, Salim Bouzebda
Preprint
arXiv, 2026
Abstract
Multimarginal optimal transport (MOT) has gained increasing attention in recent years, notably due to its relevance in machine learning and statistics, where one seeks to jointly compare and align multiple probability distributions. This paper presents a unified and complete Kantorovich duality theory for MOT problem on general Polish product spaces with bounded continuous cost function. For marginal compact spaces, the duality identity is derived through a convex-analytic reformulation, that identifies the dual problem as a Fenchel-Rockafellar conjugate. We obtain dual attainment and show that optimal potentials may always be chosen in the class of $c$-conjugate families, thereby extending classical two-marginal conjugacy principle into a genuinely multimarginal setting. In non-compact setting, where direct compactness arguments are unavailable, we recover duality via a truncation-tightness procedure based on weak compactness of multimarginal transference plans and boundedness of the cost. We prove that the dual value is preserved under restriction to compact subsets and that admissible dual families can be regularized into uniformly bounded $c$-conjugate potentials. The argument relies on a refined use of $c$-splitting sets and their equivalence with multimarginal $c$-cyclical monotonicity. We then obtain dual attainment and exact primal-dual equality for MOT on arbitrary Polish spaces, together with a canonical representation of optimal dual potentials by $c$-conjugacy. These results provide a structural foundation for further developments in probabilistic and statistical analysis of MOT, including stability, differentiability, and asymptotic theory under marginal perturbations.
Optimal Transport Guarantees to Nonparametric Regression for Locally Stationary Time Series
Jan N. Tinio, Mokhtar Z. Alaya, Salim Bouzebda
ConferenceAISTATS, 2026

Abstract
Locally stationary time series (LSTS) represent an essential modeling paradigm for capturing the nuanced dynamics inherent in time series data, whose statistical characteristics, including mean and variance, evolve smoothly over time. In this paper, we propose a conditional probability distribution estimator for LSTS through Nadaraya–Watson (NW) kernel smoothing. NW estimator leverages local kernel smoothing to approximate the conditional distribution of a response variable given its covariates. Under mild conditions, we establish optimal transport convergence guarantees to the proposed NW-based conditional probability estimator. These guarantees are initially proven in the univariate setting using the Wasserstein distance, and subsequently in a multivariate setting employing the sliced Wasserstein distance. To corroborate our theoretical findings, we conduct a wide range of numerical experiments to assess the convergence rates and showcase the practical relevance of the estimator in capturing intricate temporal dependencies in complex nonstationary phenomena.
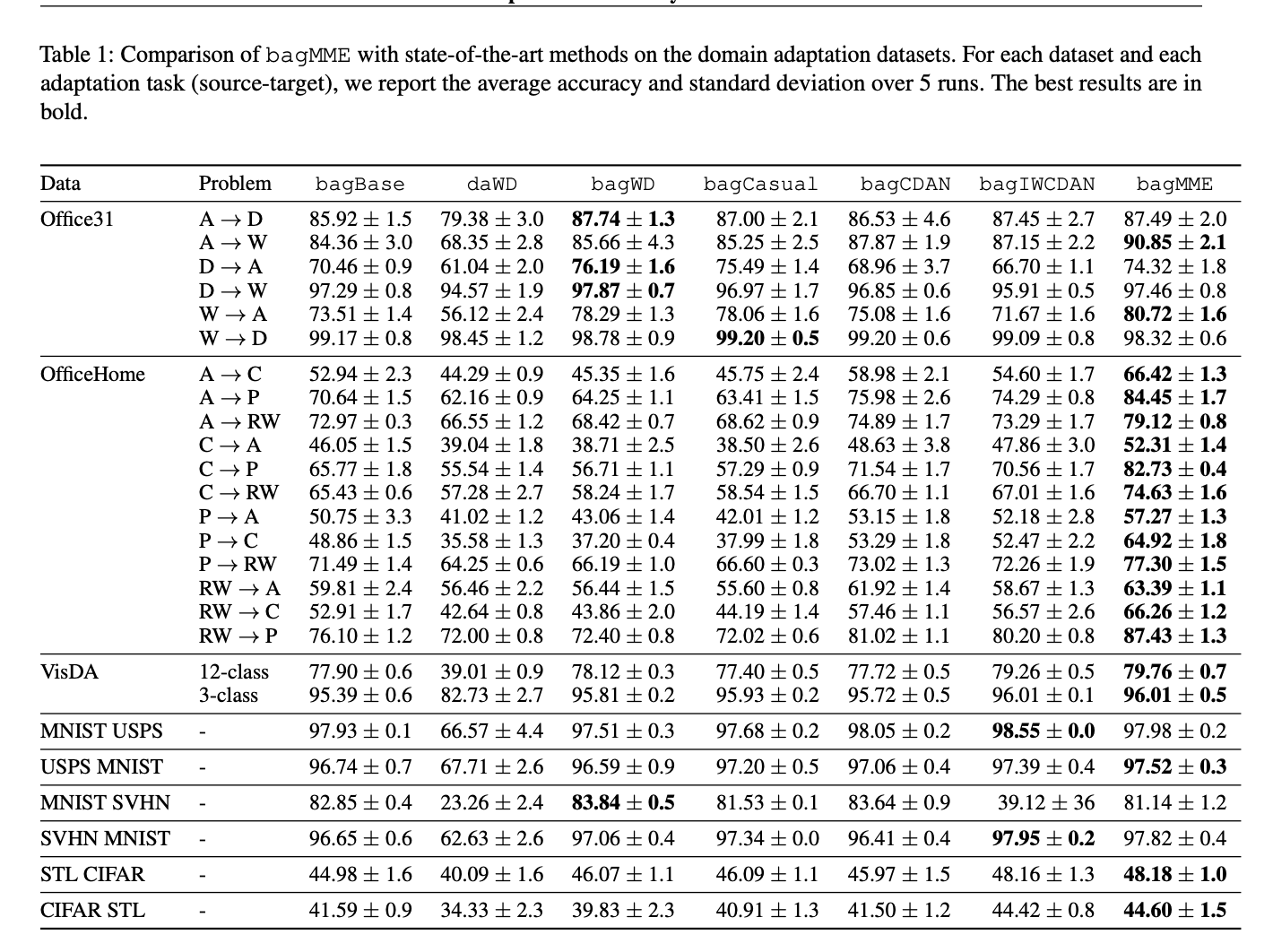
Unmixing Mean Embeddings for Domain Adaptation with Target Label Proportion
Alain Rakotomamonjy , Maxime Berar, Mokhtar Z. Alaya
ConferenceAISTATS, 2026
Abstract
We introduce a novel approach to domain adaptation within the context of Learning from Label Proportions (LLP). We address the challenging scenario where labeled samples are available in the source domain, but only bags of unlabeled samples with their corresponding label proportions are accessible in the target domain. Our proposed method, bagMME (Bag Matching Mean Embeddings), tackles the distributional shift between domains by focusing on matching class-conditional distributions. A key contribution of bagMME is a simple yet effective unmixing strategy that leverages the target label proportions to estimate the target class-conditional mean embeddings. These estimated target means are then aligned with their corresponding source class-conditional means, thereby reducing the domain discrepancy. We theoretically demonstrate the soundness of our approach and its effectiveness in mitigating distributional shifts. Extensive experiments on various computer vision datasets showcase the superior performance of bagMME compared to state-of-the-art baselines. Our results highlight the critical role of incorporating target label proportions into the learning process for improved generalization on the target domain.
Application of Convolution Neural Network for Unfolding Simulated Neutron Spectra of an Activation Spectrometer
Rodayna Hmede, Thibaut Vinchon, Quentin Ducasse, Mokhtar Z. Alaya, Wilfried Monange, Jeremy Bez
Journal IEEE Transactions on Nuclear Science, 2026
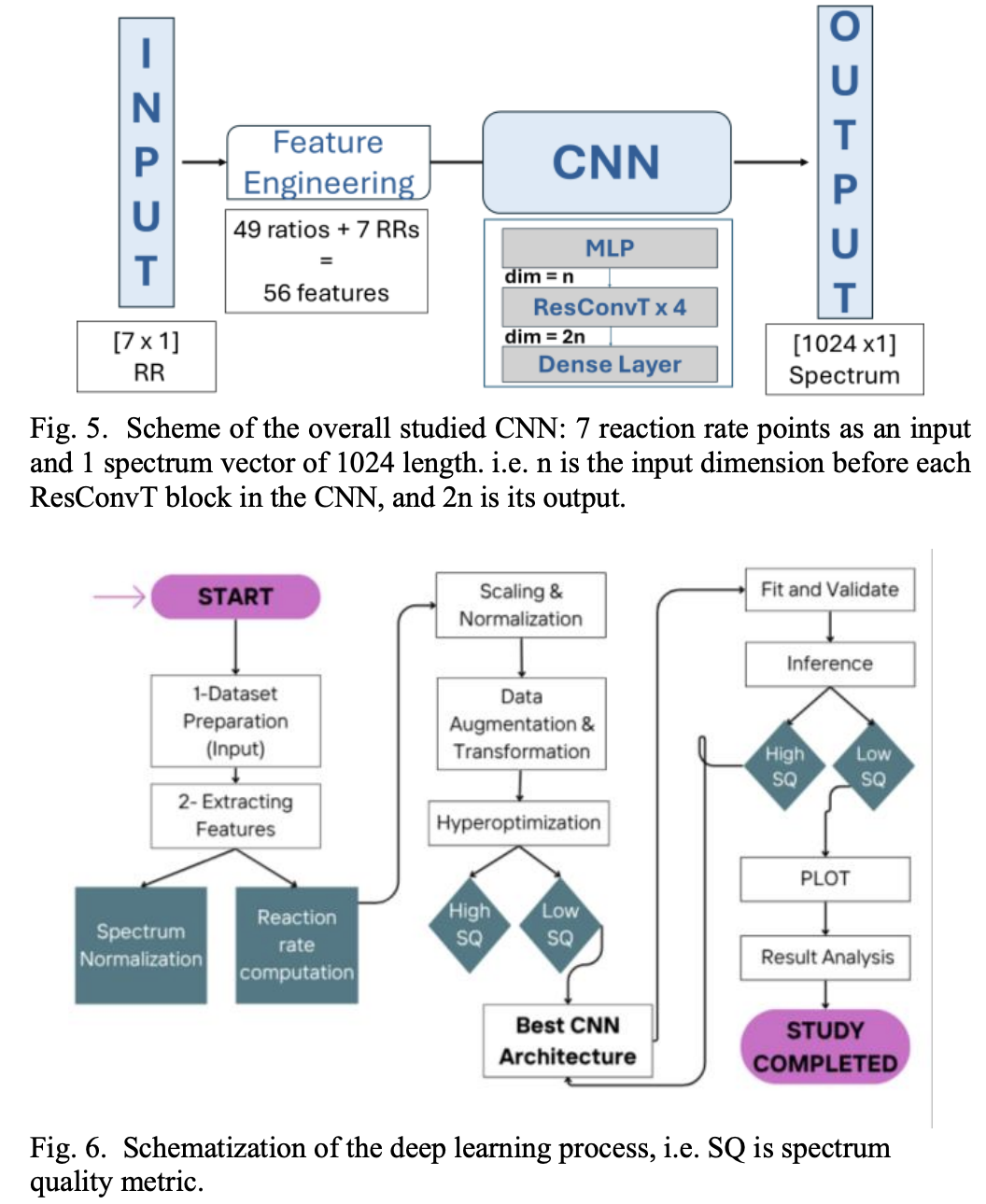
Abstract
Neutron studies are of significant interest in fields such as radiation protection, nuclear reactor physics, and criticality safety, where accurate determination of neutron field is essential. Determining the neutron field typically involves unfolding detector signals, such as those obtained from the activation and counting neutron spectrometer (SNAC) detector. Traditional methods, as Bayesian approaches, have been widely integrated for this neutron spectrum unfolding. However, these methods rely on an initial solution estimation, introducing biases or uncertainties. Recent studies in artificial intelligence (AI) have demonstrated its potential to address challenges as hysteresis regression. This work is based on our novel convolutional neural network (CNN) architecture to overcome the hysteresis problem in neutron spectrum unfolding. The CNN model predicts the neutron spectrum directly from detector counts, eliminating the need for prior solution predictions. The proposed architecture was trained on a large simulation dataset and validated through a combination of Serpent simulations of various Californium-252 (Cf) spectra and Monte Carlo N-Particles (MCNPs) simulations of the Silene reactor. These two complementary simulation approaches are used to evaluate the CNN’s evaluation in realistic neutron environments. The results demonstrate the model’s high efficiency and accuracy, as evidenced by key performance metrics and the quality of the predicted spectrum (SQ). This approach represents a significant step forward in optimizing and validating AI-based methods for neutron field, especially in criticality dosimetry and radiation protection applications. Preliminary comparisons with Bayesian unfolding codes already indicate than CNN-based predictions can capture fine spectral features. A benchmark against MAXED, GRAVEL, and Nubay remains a key perspective, together with validation campaigns on neutron facilities.
Bounds in Wasserstein Distance for Locally Stationary Functional Time Series
Jan N. G. Tinio, Mokhtar Z. Alaya, Salim Bouzebda
PreprintarXiv, 2025
Abstract
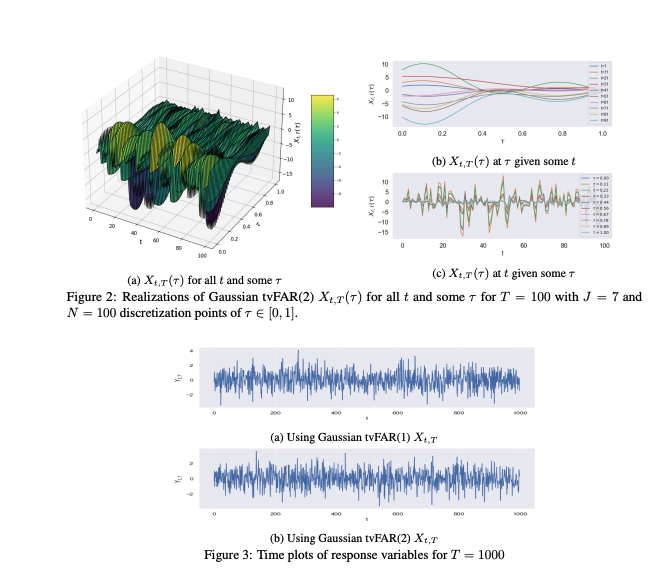
Functional time series (FTS) extend traditional methodologies to accommodate data observed as functions/curves. A significant challenge in FTS consists of accurately capturing the time-dependence structure, especially with the presence of time-varying covariates. When analyzing time series with time-varying statistical properties, locally stationary time series (LSTS) provide a robust framework that allows smooth changes in mean and variance over time. This work investigates Nadaraya-Watson (NW) estimation procedure for the conditional distribution of locally stationary functional time series (LSFTS), where the covariates reside in a semi-metric space endowed with a semi-metric. Under small ball probability and mixing condition, we establish convergence rates of NW estimator for LSFTS with respect to Wasserstein distance. The finite-sample performances of the model and the estimation method are illustrated through extensive numerical experiments both on functional simulated and real data.
Bounds in Wasserstein Distance for Locally Stationary Processes
Jan N. G. Tinio, Mokhtar Z. Alaya, Salim Bouzebda
Preprint
arXiv, 2024
Abstract
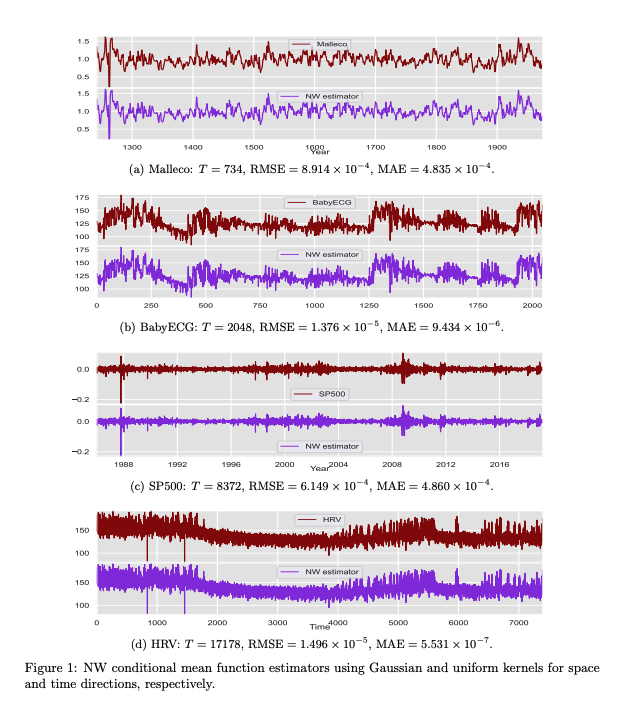
Locally stationary processes (LSPs) provide a robust framework for modeling time-varying phenomena, allowing for smooth variations in statistical properties such as mean and variance over time. In this paper, we address the estimation of the conditional probability distribution of LSPs using Nadaraya-Watson (NW) type estimators. The NW estimator approximates the conditional distribution of a target variable given covariates through kernel smoothing techniques. We establish the convergence rate of the NW conditional probability estimator for LSPs in the univariate setting under the Wasserstein distance and extend this analysis to the multivariate case using the sliced Wasserstein distance. Theoretical results are supported by numerical experiments on both synthetic and real-world datasets, demonstrating the practical usefulness of the proposed estimators.
Sparsified-Learning for Heavy-Tailed Locally Stationary
Yingjie Wang, Mokhtar Z. Alaya, Salim Bouzebda, Xinsheng Liu
Preprint
arXiv, 2025
Abstract
Sparsified Learning is ubiquitous in many machine learning tasks. It aims to regularize the objective function by adding a penalization term that considers the constraints made on the learned parameters. This paper considers the problem of learning heavy-tailed LSP. We develop a flexible and robust sparse learning framework capable of handling heavy-tailed data with locally stationary behavior and propose concentration inequalities. We further provide non-asymptotic oracle inequalities for different types of sparsity, including ℓ1-norm and total variation penalization for the least square loss.
Adversarial Semi-Supervised Domain Adaptation for Semantic Segmentation: A New Role for Labeled Target Samples
Marwa Kechaou, Mokhtar Z. Alaya, Romain Hérault, Gilles Gasso
Journal
Computer Vision and Image Understanding, 2025
Abstract
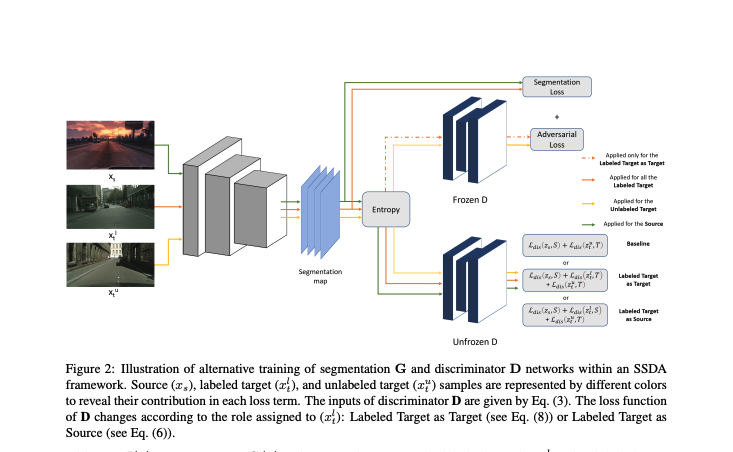
Adversarial learning baselines for domain adaptation (DA) approaches in the context of semantic segmentation are under explored in semi-supervised framework. These baselines involve solely the available labeled target samples in the supervision loss. In this work, we propose to enhance their usefulness on both semantic segmentation and the single domain classifier neural networks. We design new training objective losses for cases when labeled target data behave as source samples or as real target samples. The underlying rationale is that considering the set of labeled target samples as part of source domain helps reducing the domain discrepancy and, hence, improves the contribution of the adversarial loss. To support our approach, we consider a complementary method that mixes source and labeled target data, then applies the same adaptation process. We further propose an unsupervised selection procedure using entropy to optimize the choice of labeled target samples for adaptation. We illustrate our findings through extensive experiments on the benchmarks GTA5, SYNTHIA, and Cityscapes. The empirical evaluation highlights competitive performance of our proposed approach.
Gaussian-Smoothed Sliced Probability Divergences
Mokhtar Z. Alaya, Alain Rakotomamonjy, Maxime Bérar, Gilles Gasso
Journal
Transactions on Machine Learning Research, 2024
Abstract
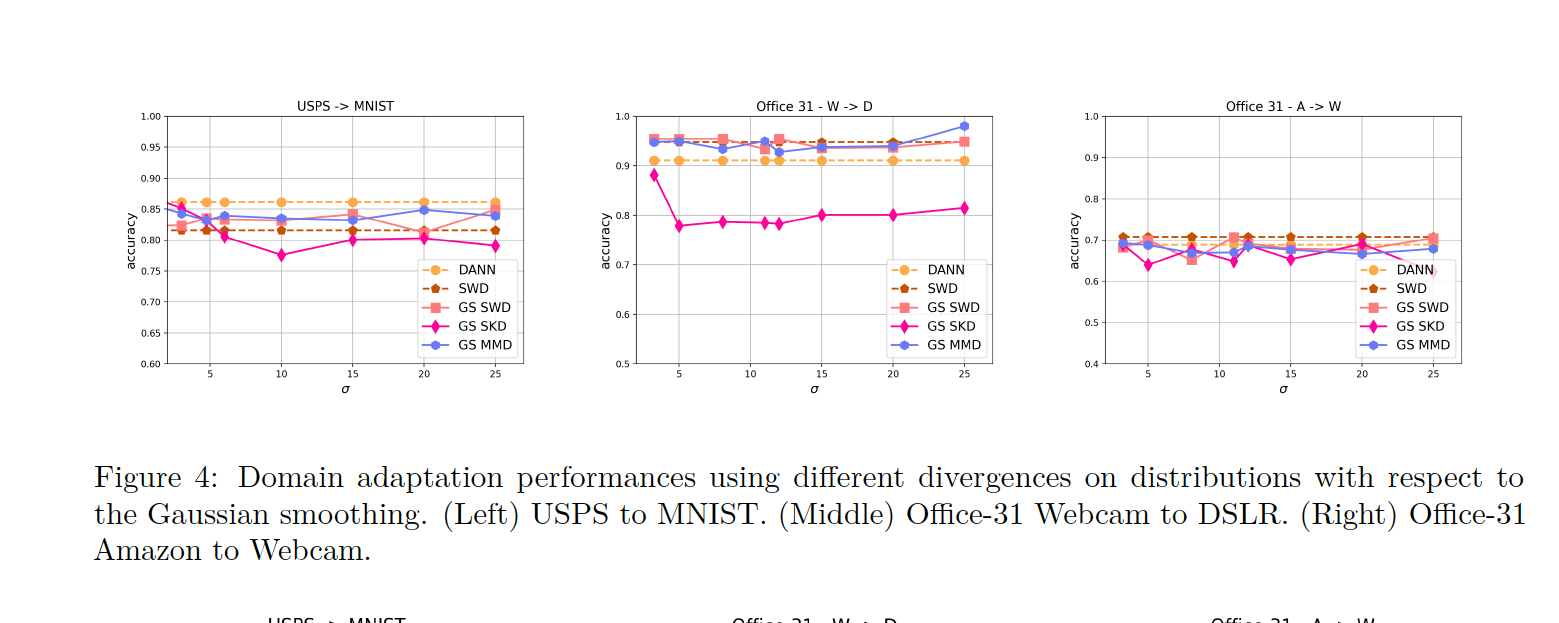
Gaussian smoothed sliced Wasserstein distance has been recently introduced for comparing probability distributions, while preserving privacy on the data. It has been shown that it provides performances similar to its non-smoothed (non-private) counterpart. However, the computational and statistical properties of such a metric have not yet been well-established. This work investigates the theoretical properties of this distance as well as those of generalized versions denoted as Gaussian-smoothed sliced divergences \(\textrm{GSD}_p\). We first show that smoothing and slicing preserve the metric property and the weak topology. To study the sample complexity of such divergences, we then introduce \(\hat{\hat\mu}_{n}\) the double empirical distribution for the smoothed-projected \(\mu\). The distribution \(\hat{\hat\mu}_{n}\) is a result of a double sampling process: one from sampling according to the origin distribution \(\mu\) and the second according to the convolution of the projection of \(\mu\) on the unit sphere and the Gaussian smoothing. We particularly focus on the Gaussian smoothed sliced Wasserstein distance \(\textrm{GSW}_p\) and prove that it converges with a rate \(O(n^{-1/{2p}})\). We also derive other properties, including continuity, of different divergences with respect to the smoothing parameter. We support our theoretical findings with empirical studies in the context of privacy-preserving domain adaptation.
Neutron Spectrum Unfolding using two Architectures of Convolutional Neural Networks
Maha Bouhadida, Asmae Mazzi, Mariya Brovchenko, Thibaut Vinchon, Mokhtar Z. Alaya, Wilfried Monange, François Trompier
Journal
Nuclear Engineering and Technology, 2023
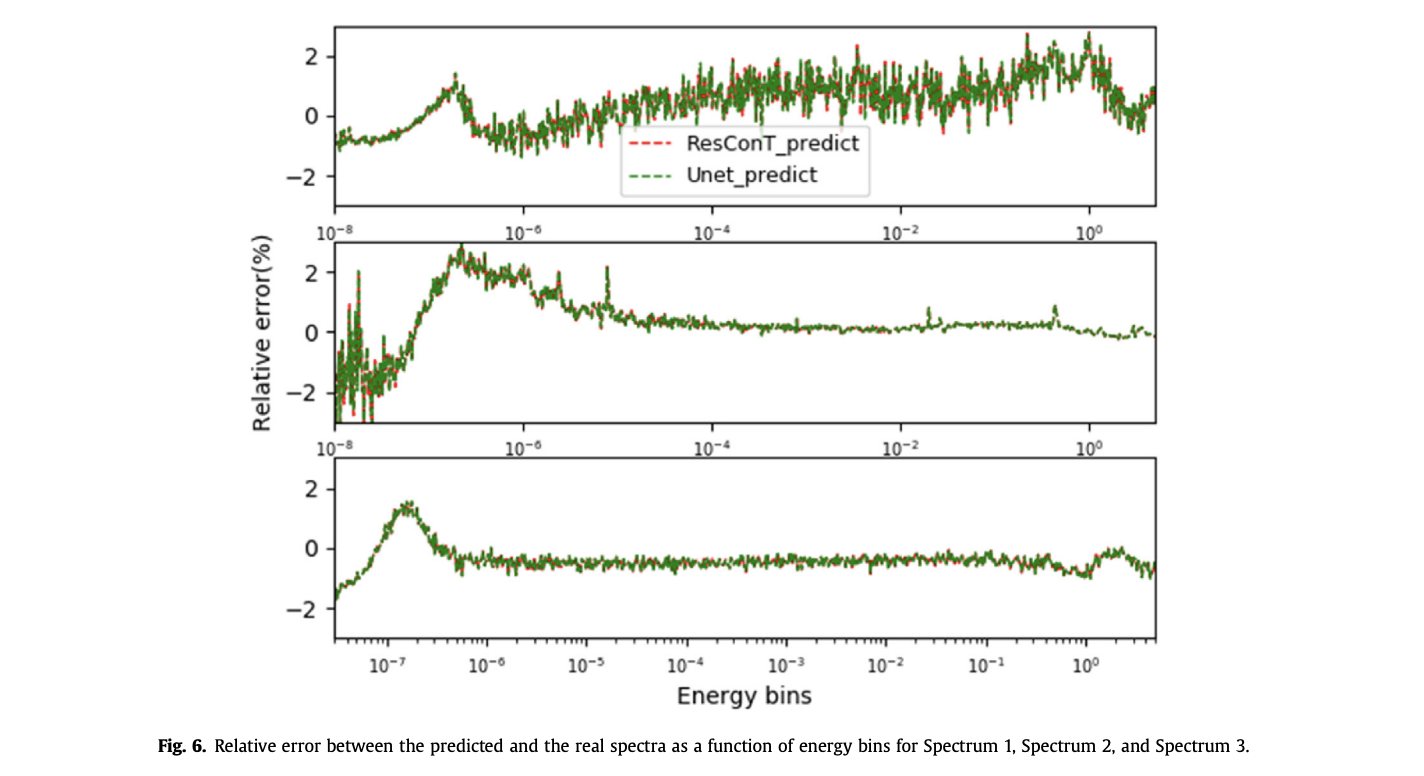
Abstract
We deploy artificial neural networks to unfold neutron spectra from measured energy-integrated quantities. These neutron spectra represent an important parameter allowing to compute the absorbed dose and the kerma to serve radiation protection in addition to nuclear safety. The built architectures are inspired from convolutional neural networks. The first architecture is made up of residual transposed convolution's blocks while the second is a modified version of the U-net architecture. A large and balanced dataset is simulated following “realistic” physical constraints to train the architectures in an efficient way. Results show a high accuracy prediction of neutron spectra ranging from thermal up to fast spectrum. The dataset processing, the attention paid to performances' metrics and the hyper-optimization are behind the architectures' robustness.
Binacox: Automatic Cut-Points Detection in High-Dimensional Cox Model, with Applications to Genetic Data
Simon Bussy, Mokhtar Z. Alaya, Anne-Sophie Jannot, Agathe Guilloux
Journal
Biometrics, 2022
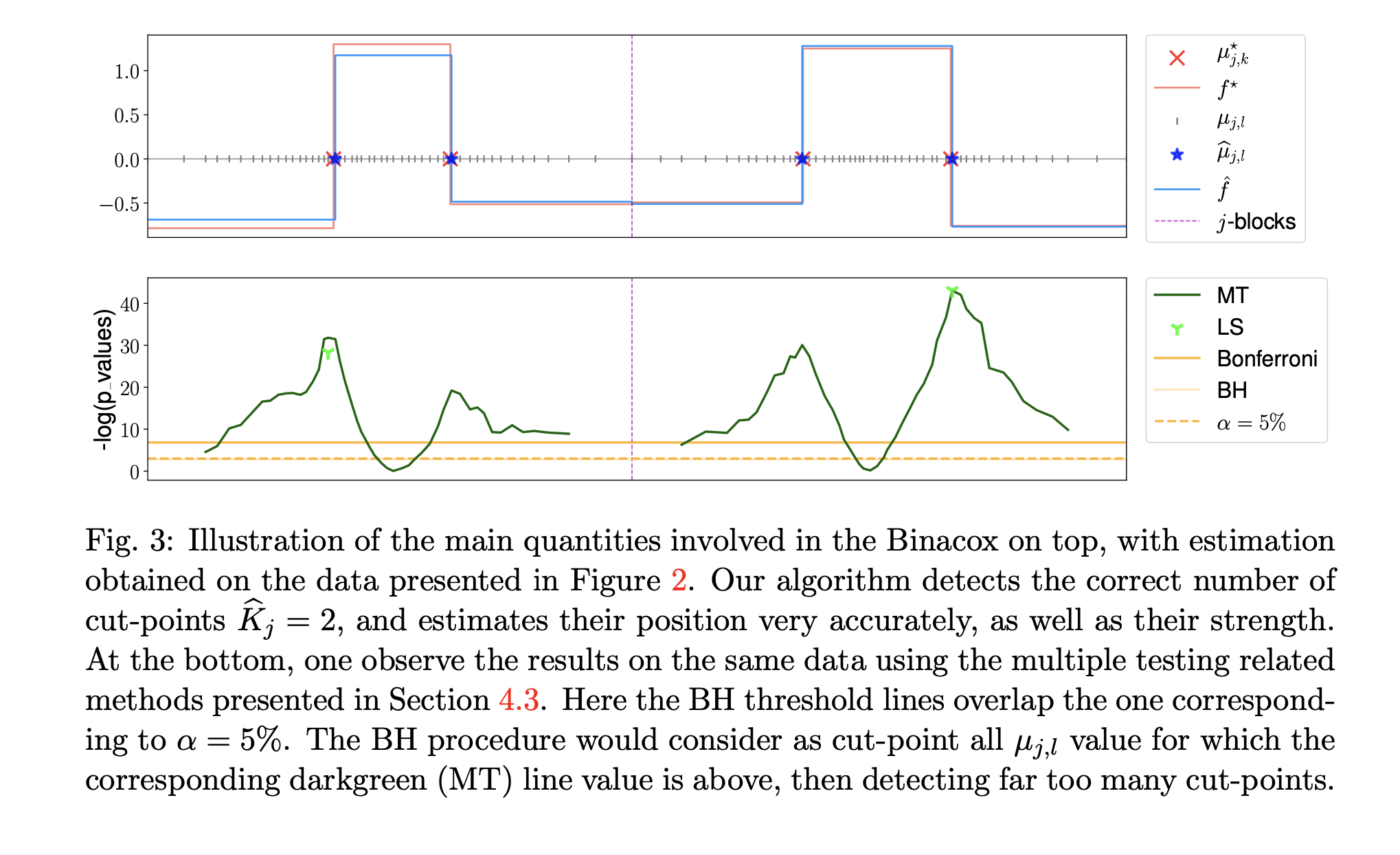
Abstract
We introduce the binacox, a prognostic method to deal with the problem of detecting multiple cut-points per features in a multivariate setting where a large number of continuous features are available. The method is based on the Cox model and combines one-hot encoding with the binarsity penalty, which uses total-variation regularization together with an extra linear constraint, and enables feature selection. Nonasymptotic oracle inequalities for prediction and estimation with a fast rate of convergence are established. The statistical performance of the method is examined in an extensive Monte Carlo simulation study, and then illustrated on three publicly available genetic cancer datasets. On these high-dimensional datasets, our proposed method significantly outperforms state-of-the-art survival models regarding risk prediction in terms of the C-index, with a computing time orders of magnitude faster. In addition, it provides powerful interpretability from a clinical perspective by automatically pinpointing significant cut-points in relevant variables.
Theoretical Guarantees for Bridging Metric Measure Embedding and Optimal Transport
Mokhtar Z. Alaya, Maxime Bérar, Gilles Gasso, Alain Rakotomamonjy
JournalNeurocomputing, 2022

Abstract
We propose a novel approach for comparing distributions whose supports do not necessarily lie on the same metric space. Unlike Gromov-Wasserstein (GW) distance which compares pairwise distances of elements from each distribution, we consider a method allowing to embed the metric measure spaces in a common Euclidean space and compute an optimal transport (OT) on the embedded distributions. This leads to what we call a sub-embedding robust Wasserstein (SERW) distance. Under some conditions, SERW is a distance that considers an OT distance of the (low- distorted) embedded distributions using a common metric. In addition to this novel proposal that generalizes several recent OT works, our contributions stands on several theoretical analyses: (i)we characterize the embedding spaces to define SERW distance for distribution alignment; (ii) we prove that SERW mimics almost the same properties of GW distance, and we give a cost relation between GW and SERW. The paper also provides some numerical illustrations of how SERW behaves on matching problems.
Screening Sinkhorn Algorithm for Regularized Optimal Transport
Mokhtar Z. Alaya, Maxime Bérar, Gilles Gasso, Alain Rakotomamonjy
ConferenceNeurIPS, 2019
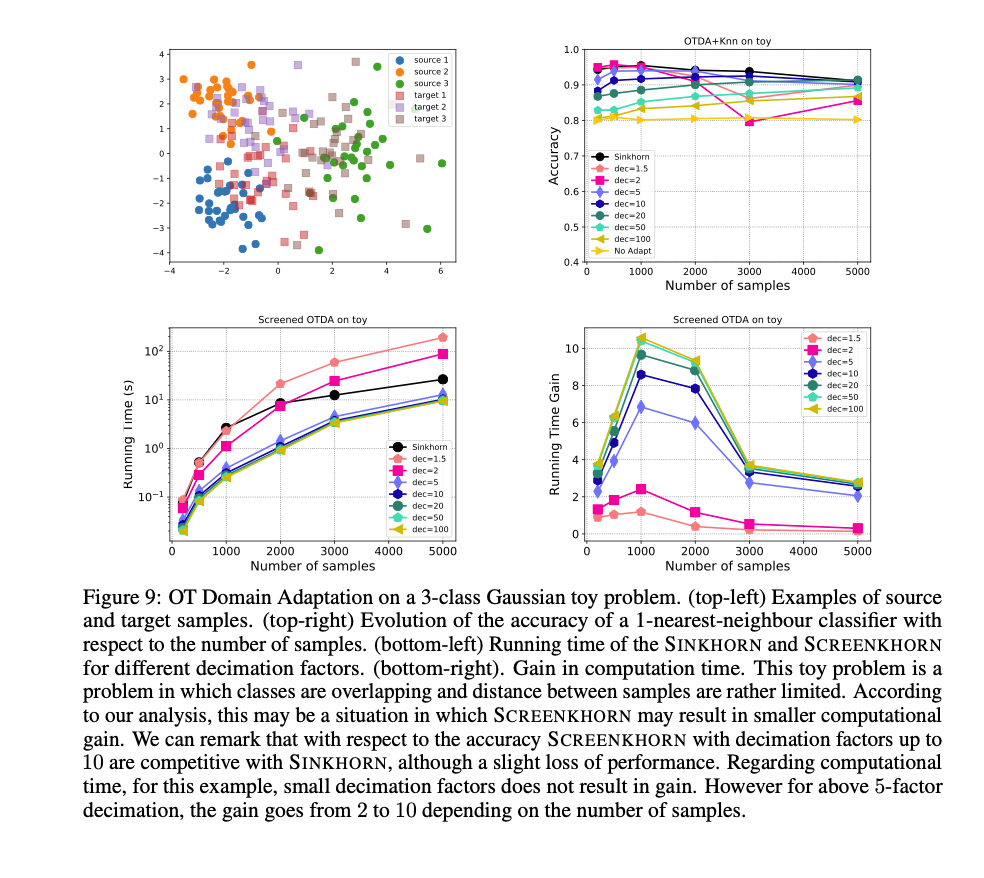
Abstract
We introduce in this paper a novel strategy for efficiently approximating the Sinkhorn distance between two discrete measures. After identifying neglectable components of the dual solution of the regularized Sinkhorn problem, we propose to screen those components by directly setting them at that value before entering the Sinkhorn problem. This allows us to solve a smaller Sinkhorn problem while ensuring approximation with provable guarantees. More formally, the approach is based on a new formulation of dual of Sinkhorn divergence problem and on the KKT optimality conditions of this problem, which enable identification of dual components to be screened. This new analysis leads to the Screenkhorn algorithm. We illustrate the efficiency of Screenkhorn on complex tasks such as dimensionality reduction and domain adaptation involving regularized optimal transport.
Heterogeneous Wasserstein Discrepancy for Incomparable Distributions
Mokhtar Z. Alaya, Maxime Bérar, Gilles Gasso, Alain Rakotomamonjy
PreprintarXiv, 2021

Abstract
Optimal Transport (OT) metrics allow for defining discrepancies between two probability measures. Wasserstein distance is for longer the celebrated OT-distance frequently-used in the literature, which seeks probability distributions to be supported on the same metric space. Because of its high computational complexity, several approximate Wasserstein distances have been proposed based on entropy regularization or on slicing, and one-dimensional Wassserstein computation. In this paper, we propose a novel extension of Wasserstein distance to compare two incomparable distributions, that hinges on the idea of distributional slicing, embeddings, and on computing the closed-form Wassertein distance between the sliced distributions. We provide a theoretical analysis of this new divergence, called heterogeneous Wasserstein discrepancy (HWD), and we show that it preserves several interesting properties including rotation-invariance. We show that the embeddings involved in HWD can be efficiently learned. Finally, we provide a large set of experiments illustrating the behavior of HWD as a divergence in the context of generative modeling and in query framework.
POT: Python Optimal Transport
Rémi Flamary, Nicolas Courty, Alexandre Gramfort, Mokhtar Z. Alaya, Aurélie Boisbunon, Stanislas Chambon, Laetitia Chapel, Adrien Corenflos, Kilian Fatras, Nemo Fournier, Léo Gautheron, Nathalie T.H. Gayraud, Hicham Janati, Alain Rakotomamonjy, Ievgen Redko, Antoine Rolet, Antony Schutz, Vivien Seguy, Danica J. Sutherland, Romain Tavenard, Alexander Tong, Titouan Vayer;
Journal
Journal of Machine Learning Research, 2021
Abstract
Optimal transport has recently been reintroduced to the machine learning community thanks in part to novel efficient optimization procedures allowing for medium to large scale applications. We propose a Python toolbox that implements several key optimal transport ideas for the machine learning community. The toolbox contains implementations of a number of founding works of OT for machine learning such as Sinkhorn algorithm and Wasserstein barycenters, but also provides generic solvers that can be used for conducting novel fundamental research. This toolbox, named POT for Python Optimal Transport, is open source with an MIT license.
Open Set Domain Adaptation using Optimal Transport
Marwa Kechaou, Romain Hérault, Mokhtar Z. Alaya, Gilles Gasso
Conference
ECML-PKDD, 2020
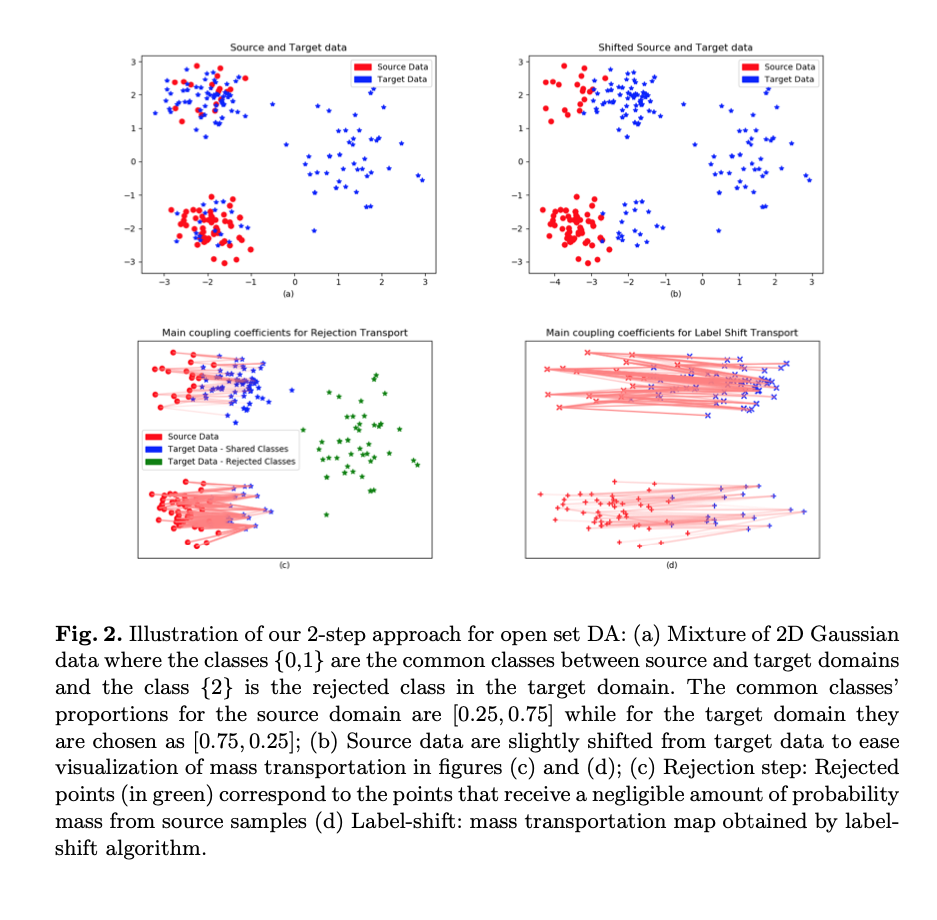
Abstract
We present a 2-step optimal transport approach that per- forms a mapping from a source distribution to a target distribution. Here, the target has the particularity to present new classes not present in the source domain. The first step of the approach aims at rejecting the samples issued from these new classes using an optimal transport plan. The second step solves the target (class ratio) shift still as an optimal transport problem. We develop a dual approach to solve the optimization problem involved at each step and we prove that our results outperform recent state-of-the-art performances. We further apply the approach to the setting where the source and target distributions present both a label- shift and an increasing covariate (features) shift to show its robustness.
Binarsity: a Penalization for One-Hot Encoded Features in Linear Supervised Learning
Mokhtar Z. Alaya, Simon Bussy, Stéphane Gaïffas, Agathe Guilloux
Journal
Journal of Machine Learning Research, 2019
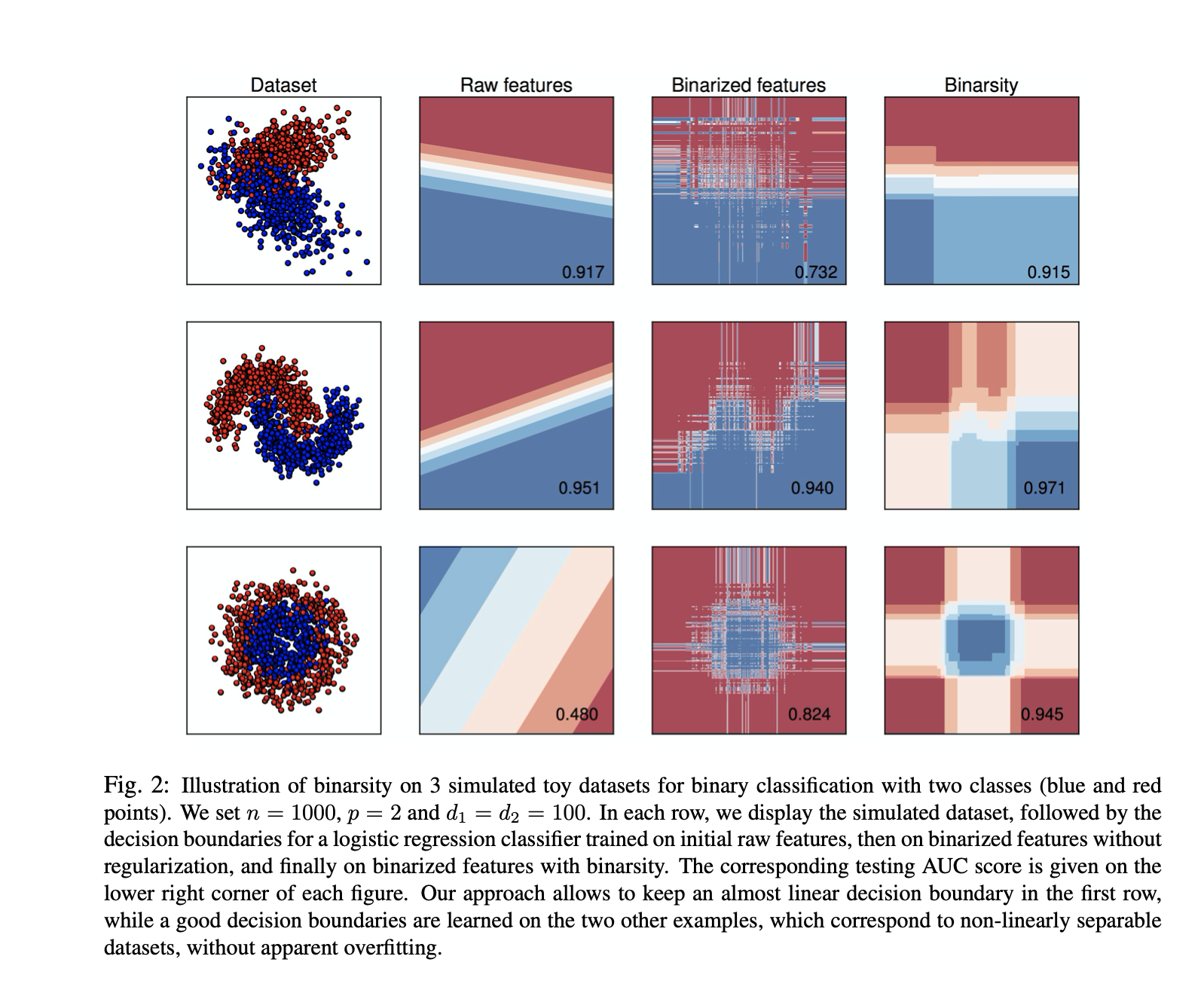
Abstract
This paper deals with the problem of large-scale linear supervised learning in settings where a large number of continuous features are available. We propose to combine the well-known trick of one-hot encoding of continuous features with a new penalization called binarsity. In each group of binary features coming from the one-hot encoding of a single raw continuous feature, this penalization uses totalvariation regularization together with an extra linear constraint. This induces two interesting properties on the model weights of the one-hot encoded features: they are piecewise constant, and are eventually block sparse. Non-asymptotic oracle inequalities for generalized linear models are proposed. Moreover, under a sparse additive model assumption, we prove that our procedure matches the state-of-the-art in this setting. Numerical experiments illustrate the good performances of our approach on several datasets. It is also noteworthy that our method has a numerical complexity comparable to standard \(\ell_1\) penalization.
Collective Matrix Completion
Mokhtar Z. Alaya, Olga Klopp
Journal
Journal of Machine Learning Research, 2019
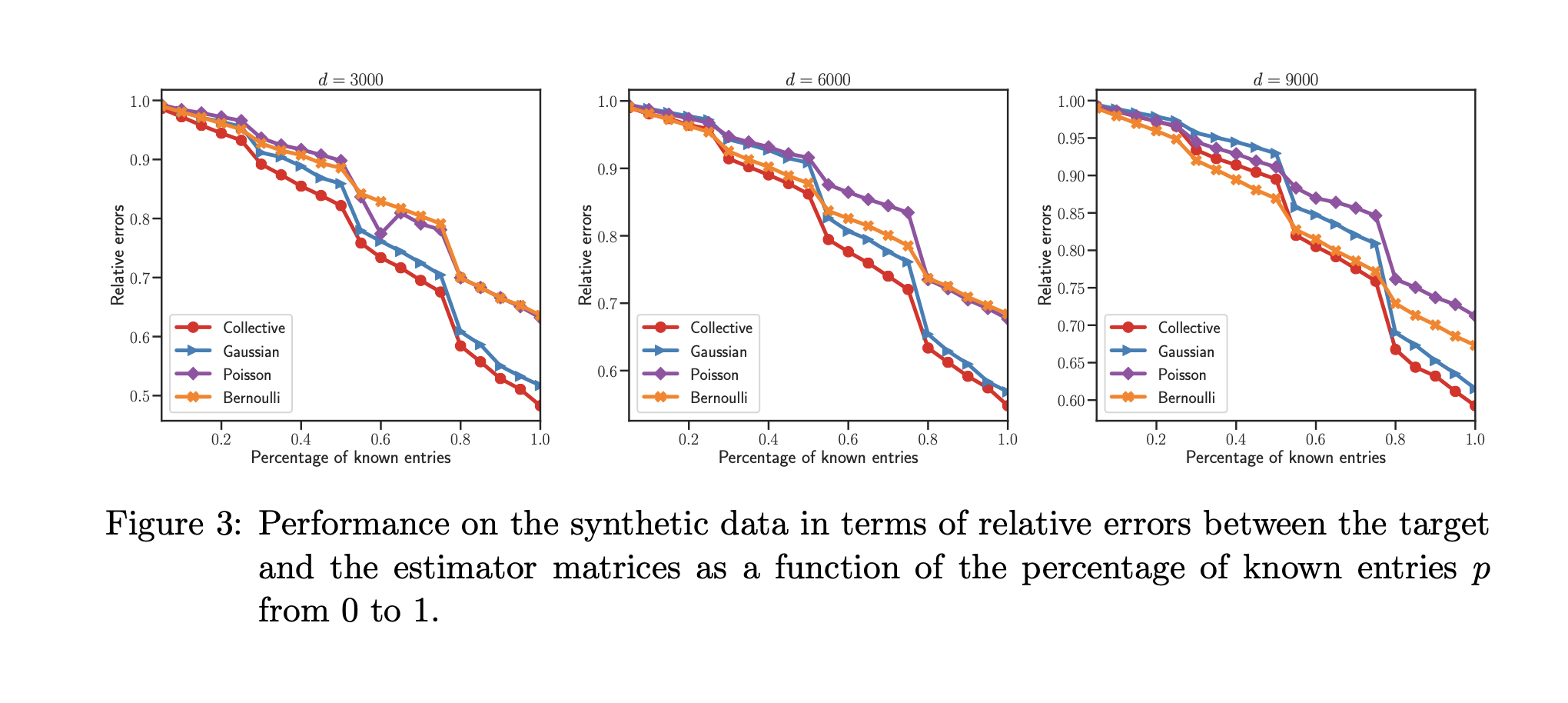
Abstract
Matrix completion aims to reconstruct a data matrix based on observations of a small number of its entries. Usually in matrix completion a single matrix is considered, which can be, for example, a rating matrix in recommendation system. However, in practical situations, data is often obtained from multiple sources which results in a collection of matrices rather than a single one. In this work, we consider the problem of collective matrix completion with multiple and heterogeneous matrices, which can be count, binary, continuous, etc. We first investigate the setting where, for each source, the matrix entries are sampled from an exponential family distribution. Then, we relax the assumption of exponential family distribution for the noise and we investigate the distribution-free case. In this setting, we do not assume any specific model for the observations. The estimation procedures are based on minimizing the sum of a goodness-of-fit term and the nuclear norm penalization of the whole collective matrix. We prove that the proposed estimators achieve fast rates of convergence under the two considered settings and we corroborate our results with numerical experiments.
Optimal Transport for Conditional Domain Matching and Label Shift
Alain Rakotomamonjy, Rémi Flamary, Gilles Gasso, Mokhtar Z. Alaya, Maxime Berar, Nicolas Courty
Journal
Machine Learning, 2021

Abstract
We address the problem of unsupervised domain adaptation under the setting of generalized target shift (joint class-conditional and label shifts). For this framework, we theoretically show that, for good generalization, it is necessary to learn a latent representation in which both marginals and class-conditional distributions are aligned across domains. For this sake, we propose a learning problem that minimizes importance weighted loss in the source domain and a Wasserstein distance between weighted marginals. For a proper weighting, we provide an estimator of target label proportion by blending mixture estimation and optimal matching by optimal transport. This estimation comes with theoretical guarantees of correctness under mild assumptions. Our experimental results show that our method performs better on average than competitors across a range domain adaptation problems including digits, VisDA and Office.
Partial Gromov-Wasserstein with Applications on Positive-Unlabeled Learning
Laetitia Chapel, Mokhtar Z. Alaya, Gilles Gasso
Conference
NeurIPS, 2020

Abstract
Classical optimal transport problem seeks a transportation map that preserves the total mass between two probability distributions, requiring their masses to be equal. This may be too restrictive in some applications such as color or shape matching, since the distributions may have arbitrary masses and/or only a fraction of the total mass has to be transported. In this paper, we address the partial Wasserstein and Gromov-Wasserstein problems and propose exact algorithms to solve them. We showcase the new formulation in a positive-unlabeled (PU) learning application. To the best of our knowledge, this is the first application of optimal transport in this context and we first highlight that partial Wasserstein-based metrics prove effective in usual PU learning settings. We then demonstrate that partial Gromov-Wasserstein metrics are efficient in scenarii in which the samples from the positive and the unlabeled datasets come from different domains or have different features.
High-Dimensional Time-Varying Aalen and Cox Models
Mokhtar Z. Alaya, Sarah Lemler, Agathe Guilloux, Thibault Allart
Preprint
arXiv, 2017
Abstract
We consider the problem of estimating the intensity of a counting process in high-dimensional time-varying Aalen and Cox models. We introduce a covariate-specific weighted total-variation penalization, using data-driven weights that correctly scale the penalization along the observation interval. We provide theoretical guaranties for the convergence of our estimators and present a proximal algorithm to solve the convex studied problems. The practical use and effectiveness of the proposed method are demonstrated by simulation studies and real data example.
Learning the Intensity of Time Events with Change-Points
Mokhtar Z. Alaya, Stéphane Gaïffas, Agathe Guilloux
Journal
IEEE Transactions on Information Theory, 2015
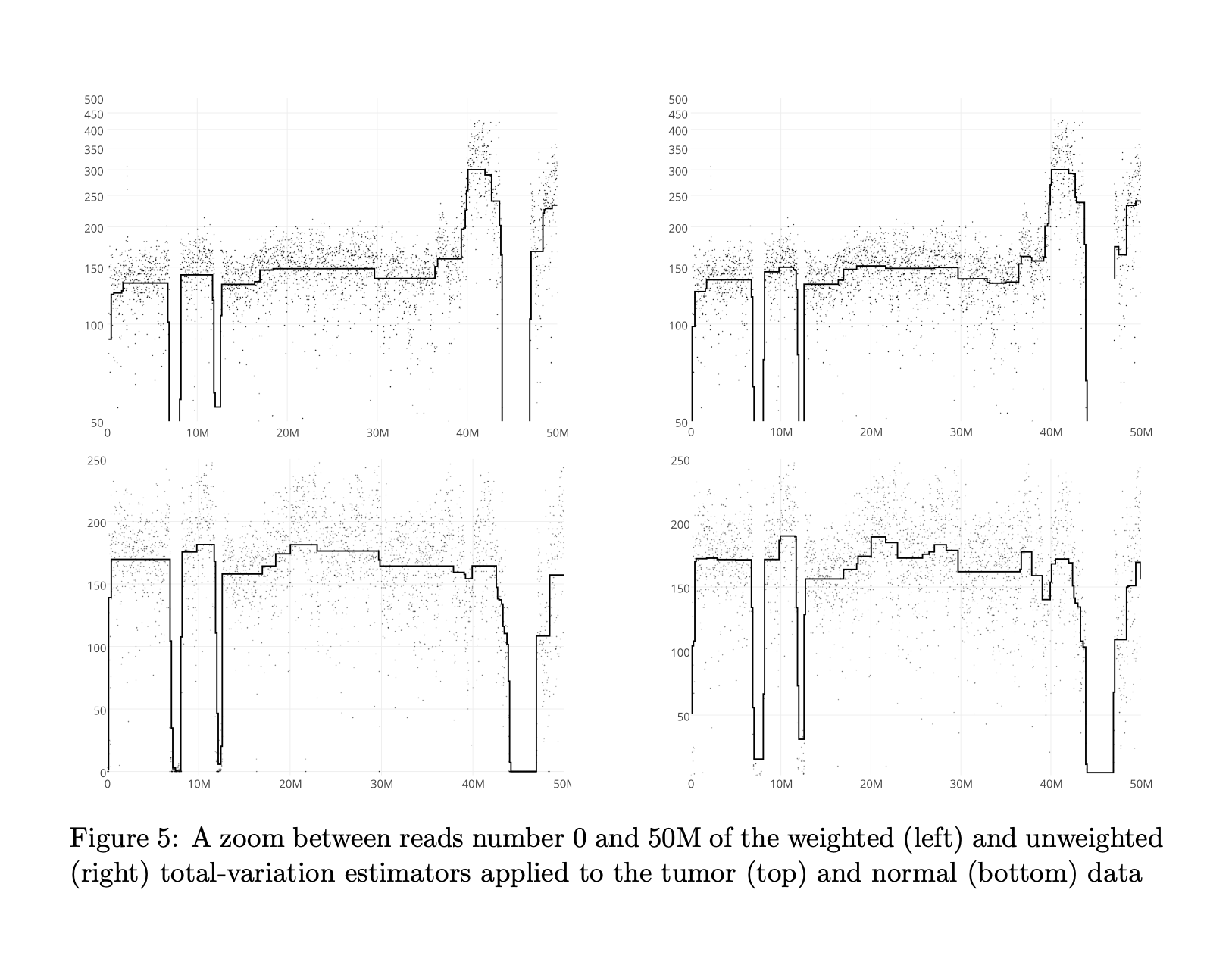
Abstract
We consider the problem of learning the inhomogeneous intensity of a counting process, under a sparse segmentation assumption. We introduce a weighted total-variation penalization, using data-driven weights that correctly scale the penalization along the observation interval. We prove that this leads to a sharp tuning of the convex relaxation of the segmentation prior, by stating oracle inequalities with fast rates of convergence, and consistency for change-points detection. This provides first theoretical guarantees for segmentation with a convex proxy beyond the standard i.i.d signal + white noise setting. We introduce a fast algorithm to solve this convex problem. Numerical experiments illustrate our approach on simulated and on a high-frequency genomics dataset.
Students
PhD
- UTC
- co-supervision with Salim Bouzebda
- title: Multimarginal Optimal Transport
- INSA Rouen
- co-supervision with Gilles Gasso
- title: Robust Deep Learning Anomaly Detection Applied to Intrusion Detection for Electric Vehicle Charging Points
- UTC
- co-supervision with Salim Bouzebda
- title: Fréchet Regression for Non-Euclidean Data
- School of Mathematics, Nanjing University of Aeronautics and Astronautics, China
- co-supervision with Salim Bouzebda
- title: Sparsified Learning for Heavy-Tailed Locally Stationary Time Series
Yehya Cheryala (2025-)
Samy Vilhes (2024-)
Noura Omar (2023-)
Yingjie Wang (Visiting PhD Student, 2023)
Alumni
Jan N. Tinio (2022-2025)
- UTC
- co-supervision with Salim Bouzebda
- title: Learning Local Stationary Processes through Wasserstein Distance
- Now Assistant Professor at Caraga State University, Phillipines
Master 2
- ESCOM, UTC
- co-supervision with Claire Ceballos (ESCOM) and Salim Bouzebda
- title: Artificial Intelligence-Assisted Organic Synthesis for Green Chemistry
Thierry Noehser, 2025
- Sorbonne Université, Campus Sciences & Ingénierie
- title: Graph Neural Network with Optimal Transport
Yihua Gao, 2023
Engineers (3-month internship)
Enzo Ephrem, Mouad Lemhadre, Zakaria Sriti, 2025, UTC, Diffusion Models for Medical Anomaly Detection
Dartois Evan, Cyprien Chenain, 2025, UTC, DeepSportMatch: Deep Recommendation System for Matching Sport Profiles
Nermine Sboui, Mohamed H. Benboubker, 2025, UTC, Diffusion Models for Anomaly Detection in Time Series
Alexandre Bidaux, Clement Martins, 2025, UTC, Paris Metro Traffic: Analysis, Prediction and Statistics
Imene Banyagoub, Massil Bouzar, Saad Lakramti, 2023, UTC, Domain Adapation in Deep Learning
Damien Dieudonné, Eloise Moreira, 2023, UTC, IOS Application of Dog Race Classification through Deep Learning and Swift
Anne-Soline Guilbert-Ly, Jinghao Yang, Malena Zaragoza-Meran, 2023, UTC, Medical Image Segmentation with Deep Learning
Selected recent talks
International Conference on Applied Mathematics, ICOMA 3

- Optimal Transport in Machine Learning
- Djerba, December 2025
Journée Scientifique, Chaire Industrielle SAFE AI

- L’IA au LMAC : Sciences de Données avec Transport Optimal
- University of Technology of Compiègne, October 2022
SIAM conference on Mathematics for Data Science

- PUOT: Partial Optimal Transport with Applications on Positive-Unlabeled Learning
- Hybrid Conference, September 2022
Journées MAS 2022 de SMAI

- Binarsity
- Rouen, France, August 2022
Séminaire Groupe de travail Machine Learning and Massive Data Analysis, Centre Borelli ENS-PARIS SACLAY

- Collective Matrix Completion
- Centre Borelli, ENS Paris Saclay, June 2022
Séminaire Sciences de Données de l’UTC

- SCREENKHORN: Screening Sinkhorn Algorithm for Regularized Optimal Transport
- University of Technology of Compiègne, November 2020
Concours au Poste Professeur.e Assistant Monge en Apprentissage Statistique, Equipe SIMPAS, CMAP

- Candidature
- CMAP, Polytechnique, Juin 2020
Séminaire CMAP

- SCREENKHORN: Screening Sinkhorn Algorithm for Regularized Optimal Transport
- CMAP, Polytechnique, Juin 2020
Séminaire de Recrutement au Poste de Professeur en Machine Learning / Statistique

- Candidature
- CREST Rennes, Mai 2020
Summer School on Applied Harmonic Analysis and Machine Learning

- Screenkhorn: Screening Sinkhorn Algorithm for Regularized Optimal Transport
- Genoa, Italy, September 2019
Students
PhD
- INSA Rouen
- co-supervision with Gilles Gasso
- title: Robust Deep Learning Anomaly Detection Applied to Intrusion Detection for Electric Vehicle Charging Points
- University of Technology of Compiègne
- co-supervision with Salim Bouzebda
- title: Fréchet Regression for Non-Euclidean Data
- University of Technology of Compiègne
- co-supervision with Salim Bouzebda
- title: Learning Local Stationary Processes through Wasserstein Distance
- School of Mathematics, Nanjing University of Aeronautics and Astronautics, China
- co-supervision with Salim Bouzebda
- title: Sparsified Learning for Heavy-Tailed Locally Stationary Time Series
Samy Vilhes (2024-)
Noura Omar (2023-)
Jan N. Tinio (2022-)
Yingjie Wang (Visiting PhD Student, 2023)
Master 2
- Sorbonne Université, Campus Sciences & Ingénierie
- title: Graph Neural Network with Optimal Transport
Yihua GAO 2023
Engineers (3-month internship)
- University of Technology of Compiègne
- title: Domain Adapation in Deep Learning
- University of Technology of Compiègne
- title: IOS Application of Dog Race Classification through Deep Learning and Swift
- University of Technology of Compiègne
- title: Medical Image Segmentation with Deep Learning
Imene Banyagoub, Massil Bouzar, and Saad Lakramti, 2023
Damien Dieudonné and Eloise Moreira, 2023
Anne-Soline Guilbert-Ly, Jinghao Yang, and Malena Zaragoza-Meran, 2023
Services
Conference Reviewer
- NeurIPS: 2025, 2024, 2023, 2022, 2021, 2020
- ICLR: 2025, 2024, 2023, 2022
- ICML: 2025, 2024, 2023
- AISTATS: 2025, 2021
- AAAI: 2025
Journal Reviewer
- Pattern Recognition: 2025
- Neurocomputing: 2025, 2023, 2022
- JMLR: 2023, 2020
- IEEE Transactions on PAMI: 2025, 2023, 2022, 2021
- Biometrical Journal: 2022
- SIAM Journal on Mathematics of Data Science: 2025
- Image and Vision Computing: 2023
- Entropy: 2023
Consulting
Je propose une expertise en machine learning, deep learning, statistique, big data, science des données et domaines connexes. Contactez-moi pour discuter.
Contact
I work in LMAC Laboratory, Computer Science Departement, University of Technology of Compiègne.
I would be happy to talk to you if you have some ideas to discuss with me.
alayaelm@utc.frTel: (+33) 3 44 23 44 74
Office Address
Bureau GI 133, Bâtiment Plaise Pascal
Département Génie Informatique (GI)
Centre d'Innovation UTC
57 avenue de Landshut, Compiègne Cedex, 60203 France