Statistical and Topological Properties of Gaussian Smoothed Sliced Probability Divergences

A. Rakotomamonjy, M. Z. Alaya, M. Bérar, G. Gasso

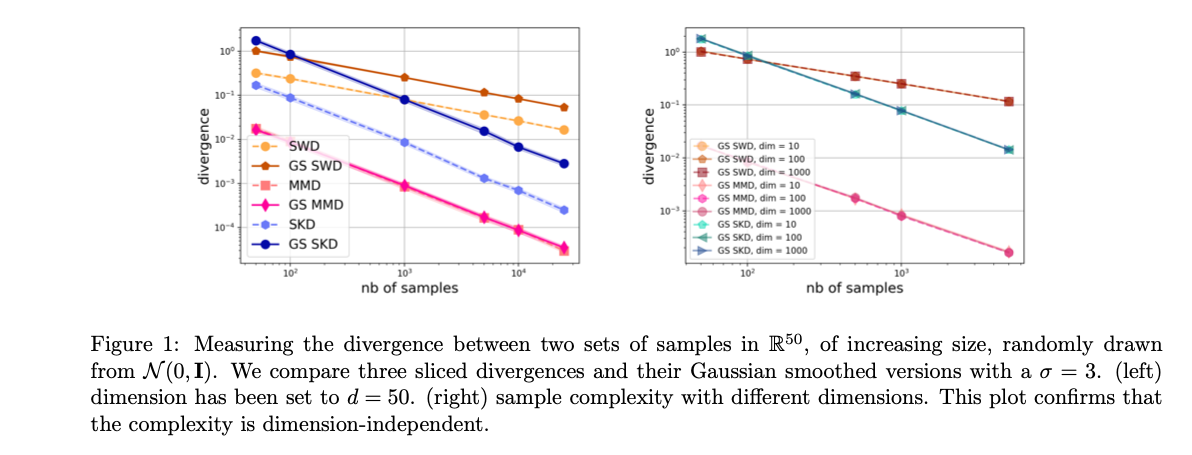
Gaussian smoothed sliced Wasserstein distance has been recently introduced for comparing probability distributions, while preserving privacy on the data. It has been shown, in applications such as domain adaptation, to provide performances similar to its non-private (non-smoothed) counter-part. However, the computational and statistical properties of such a metric is not yet been well-established. In this paper, we analyze the theoretical properties of this distance as well as those of generalized versions denoted as Gaussian smoothed sliced divergences. We show that smoothing and slicing preserve the metric property and the weak topology. We also provide results on the sample complexity of such divergences. Since, the privacy level depends on the amount of Gaussian smoothing, we analyze the impact of this parameter on the divergence. We support our theoretical findings with empirical studies of Gaussian smoothed and sliced version of Wassertein distance, Sinkhorn divergence and maximum mean discrepancy (MMD). In the context of privacy-preserving domain adaptation, we confirm that those Gaussian smoothed sliced Wasserstein and MMD divergences perform very well while ensuring data privacy. Download paper here